Monte Carlo Simulation을 이용한 Rust vs C++ vs Java vs R vs Python 벤치마크
몬테카를로 시뮬레이션(Monte Carlo Simulation)을 이용한 Rust, C++, Java, R과 Python에 대한 계산 속도 비교
유러피언 바닐라 옵션(European Vanilla Option)은 정해진 만기일에만 옵션 권리를 행사할 수 있는 옵션이다.
유러피언 옵션은 블랙-숄즈 방정식이라는 closed form으로 쉽게 구할 수 있지만 Rust, C++, Java, Python, R의 Speed Benchmark를 위하여 몬테카를로 시뮬레이션(Monte-Carlo Simulation)을 이용하여 테스트하였다.
R과 Python은 Vector 연산으로 변환하면 좀 더 빠른 계산이 가능하지만 비교를 위해 동일한 로직으로 구현하였다. 일반적으로 바닐라 옵션의 경우 시뮬레이션 횟수가 100,000 이상이면 가격이 stable하게 수렴하지만 테스트를 위해 1,000,000회까지 실시하였다.
벤치마크에 사용된 PC의 사양
* MacOS High Sierra
* Processor : 2.4GHz Intel Core i5
* Memory : 8 GB 1333 MHz DDR3
Version
| 언어 | Version | |
|---|---|---|
| Python | 3.6.4 | |
| R | 3.3.1 | |
| Java | 1.8 | |
| C++ | g++ 4.2.1 | |
| Rust | 1.47.0 |
C++는 컴파일할 때 -o3 옵션을 사용하였고 Rust는 opt-level 3를 적용했다.
Result
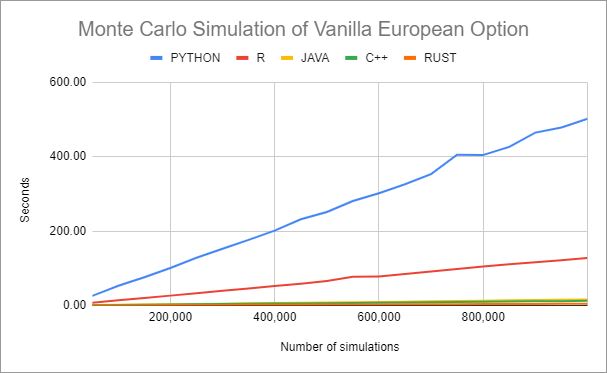
Python은 for문에 약하다는 말을 입증하듯 500,000회에 251.36초, 1,000,000회에 무려 501.97초가 걸렸다.
옵션가격에서 일반적으로 설정하는 100,000회 기준으로 Python은 53.03초, R은 14.23초, Java 1.83초, C++ 0.6초, Rust는 0.22초가 각각 소요됬다.
의외로 R이 Python보다 훨씬 빨랐다. 50,000회 7.12초, 500,000회 65.72초, 1,000,000회 127.67초가 걸렸다.
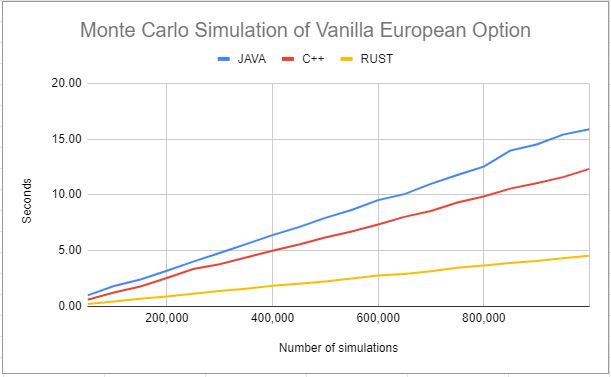
Rust는 50,000회 계산에 0.22초, 500,000회 2.23초, 1,000,000회에 4.53초가 소요됬다. Java는 예상보다 속도가 빨랐는데 윈도우10 환경에서는 최적화하지 않은 C++보다 빨랐다. 멀티 쓰레드를 반영할 경우 결과가 달라질 수도 있을 것이다.
| Simulation | 50,000 | 200,000 | 400,000 | 600,000 | 800,000 | 1,000,000 |
|---|---|---|---|---|---|---|
| PYTHON | 25.89 | 100.80 | 201.07 | 301.64 | 404.28 | 501.97 |
| R | 7.12 | 26.43 | 52.15 | 77.99 | 104.83 | 127.67 |
| JAVA | 1.00 | 3.20 | 6.39 | 9.53 | 12.54 | 15.89 |
| C++ | 0.60 | 2.56 | 4.99 | 7.34 | 9.85 | 12.33 |
| RUST | 0.22 | 0.90 | 1.85 | 2.78 | 3.66 | 4.53 |
(seconds)
Source code
Python
import time
from numpy import power, sqrt, exp
from scipy.stats import norm
class McVanillaOption:
def __init__(self, opType, S, X, T, rf, d, sigma, step_number=100, sim_number=100):
self.opType = opType
self.S = S
self.X = X
self.T = T
self.rf = rf
self.d = d
self.sigma = sigma
self.step_number = step_number
self.sim_number = sim_number
def price(self):
dt = self.T / self.step_number
drift = (self.rf - self.d - (power(self.sigma, 2) / 2)) * dt
sqrdt = self.sigma * sqrt(dt)
sum = 0
if self.opType.upper() == "CALL":
z = 1
else:
z = -1
# numpy.random.normal is slightly faster than scipy.stats.norm.rvs
for i in range(self.sim_number):
St = self.S
Wt = norm.rvs(0, 1, self.step_number)
for j in range(self.step_number):
St = St * exp(drift + sqrdt * Wt[j])
sum = sum + max(z * (St - self.X), 0)
return exp(-self.rf * self.T) * (sum / self.sim_number)
if __name__ == "__main__":
for i in range(1,21):
number = i*50000
start = time.time()
result = McVanillaOption("call", 102, 100, 0.25, 0.1, 0.05, 0.2, 100, number).price()
print("simulation : {} / price : {} / time: {}".format(number, result, time.time() - start))
R
MC_vanilla = function( flag=c("c","p") , s, x, t, r, b, sigma, nStep, nSim){
dt=t/nStep
drift=(r-b-sigma^2/2)*dt
vSqrdt=sigma*sqrt(dt)
sum=0
if (flag=='c'){
z=1
} else {
z=-1
}
for (i in 1:nSim){
st=s
wt<-rnorm(nStep)
for (j in 1:nStep){
#st=st*exp(drift+vSqrdt*rnorm(1))
st=st*exp(drift+vSqrdt*wt[j])
}
sum = sum + pmax(z*(st-x),0)
}
result=exp(-r*t)*(sum/nSim)
return(result)
}
for (i in 1:20){
number = i*50000
start_time <- Sys.time()
result = MC_vanilla("c", 102, 100, 0.25, 0.1, 0.05, 0.2, 100, number)
end_time <- Sys.time()
print(paste0("simulation : ", format(number, scientific = FALSE), " / time : ", end_time-start_time))
}
JAVA
import java.util.Random;
public class MonteCarlo {
public static double MonteCarloVanillaOption(String flag, double S, double X, double T, double rf, double d, double sigma, int nStep, long simul_number) {
double result = 0.0;
double dt = T/nStep;
double drift = (rf - d - (Math.pow(sigma,2)/2))*dt;
double vSqrdt = sigma*Math.sqrt(dt);
double sum = 0.0;
double St = 0.0;
Random random = new Random();
double z = 1.0;
if ("C".equals(flag)) {
z = 1.0;
} else {
z = -1.0;
}
for (int i=0; i<simul_number; i++) {
St = S;
for(int j=0; j<nStep; j++) {
St = St*Math.exp(drift+vSqrdt*random.nextGaussian());
}
sum += Math.max(z*(St-X), 0);
}
return Math.exp(-rf*T)*(sum/simul_number);
}
public static void main(String[] args) {
for (int i=1; i<21; i++) {
long number = i*50000L;
long start = System.currentTimeMillis();
double result = MonteCarloVanillaOption("C", 102.0, 100.0, 0.25, 0.1, 0.05, 0.2, 100, number);
long end = System.currentTimeMillis();
System.out.println(" number : " + number + " / price : " + result + " / time :" + (end-start)/1000.0 + " seconds");
}
}
}
C++
#include <iostream>
#include <cmath>
#include <random>
#include <time.h>
#include <array>
using namespace std;
double monte_carlo_vanilla_option(char optype, double S, double X, double T, double rf, double d, double sigma, int nStep, long simul_number) {
double result = 0.0;
double dt = T/nStep;
double drift = (rf - d - (pow(sigma, 2)/2))*dt;
double vsqrdt = sigma*sqrt(dt);
double sum = 0.0;
double St = 0.0;
default_random_engine generater;
normal_distribution<double> distribution(0.0, 1.0);
double z = 1.0;
if (optype=='c') {
z = 1.0;
} else {
z= -1.0;
}
for (int i=0; i<simul_number; i++) {
St = S;
for (int j=0; j<nStep; j++) {
St = St*exp(drift+vsqrdt*distribution(generater));
}
sum += max(z*(St-X), 0.0);
}
return exp(-rf*T)*(sum/simul_number);
}
int main() {
for (int i = 1; i<21; i++) {
clock_t start, end;
double times;
start = clock();
long number = i*50000L;
double result = monte_carlo_vanilla_option('c', 102.0, 100.0, 0.25, 0.1, 0.05, 0.2, 100, number);
end = clock();
cout <<"number : "<<number<<" / time : "<< ((double)(end-start))/CLOCKS_PER_SEC <<" seconds"<<endl;
}
return 0;
}
RUST
use rand_distr::{Normal, Distribution};
use std::time::{Duration, Instant};
fn monte_carlo_vanilla_option(optype: char, S: f32, X: f32, T: f32, rf: f32, d: f32, sigma: f32, nStep: i32, simul_number: i32) -> f32 {
let mut result:f32 = 0.0;
let dt: f32 = T/(nStep as f32);
let drift: f32 = (rf-d-(sigma.powf(2.0)/2.0))*dt;
let vsqrtdt: f32 = dt.sqrt()*sigma;
let mut sum: f32 = 0.0;
let mut St: f32 = 0.0;
let mut z: f32 = 0.0;
let normal = Normal::new(0.0, 1.0).unwrap();
if optype =='c' {
z = 1.0;
} else {
z = - 1.0;
}
for i in 0..simul_number {
St = S;
for j in 0..nStep {
St = (drift+vsqrtdt*normal.sample(&mut rand::thread_rng())).exp()*St;
}
sum = sum + (z*(St-X)).max(0.0);
}
return (-rf*T).exp()*(sum/(simul_number as f32));
}
fn main() {
for i in 1..21 {
let mut start = Instant::now();
let mut number = i*50000;
let mut result = monte_carlo_vanilla_option('c', 102.0, 100.0, 0.25, 0.1, 0.05, 0.2, 100, number);
let mut duration = start.elapsed();
println!("simulation {} / value : {} / time {:?}", number, result, duration);
}
}
Cargo.toml
[dependencies]
rand = "0.7.3"
rand_distr = "0.3.0"
[profile.dev]
opt-level = 0
[profile.release]
opt-level = 3
- Build
cargo build --release
- 실행
cargo run --release